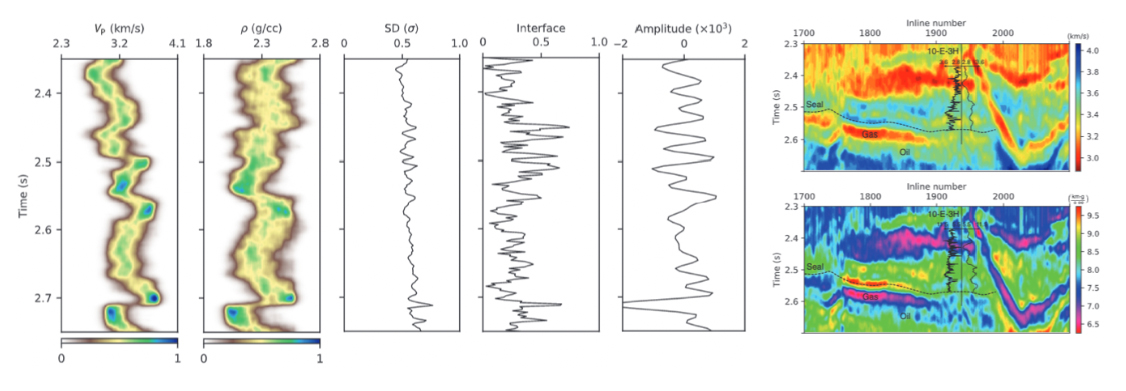
We have used a transdimensional form of MCMC, reversible jump MCMC, to estimate seismic impedance, which allows the inference of the number of interfaces as well as the interface location and layer impedances. Estimating the uncertainty quantitatively is also very important when performing stochastic inversion. Therefore, the goal of this research is to apply the transdimensional method to obtain a 3D seismic impedance model and to quantify uncertainty in impedance and interface locations. We used seismic data from the E-segment of the Norne field in Norwegian Sea. The results of the quasi 3D transdimensional MCMC approach, which independently inverts data from each common-depth-point location, indicate high velocity contrasts near gas-oil contacts and high uncertainty in impedance near discontinuities.

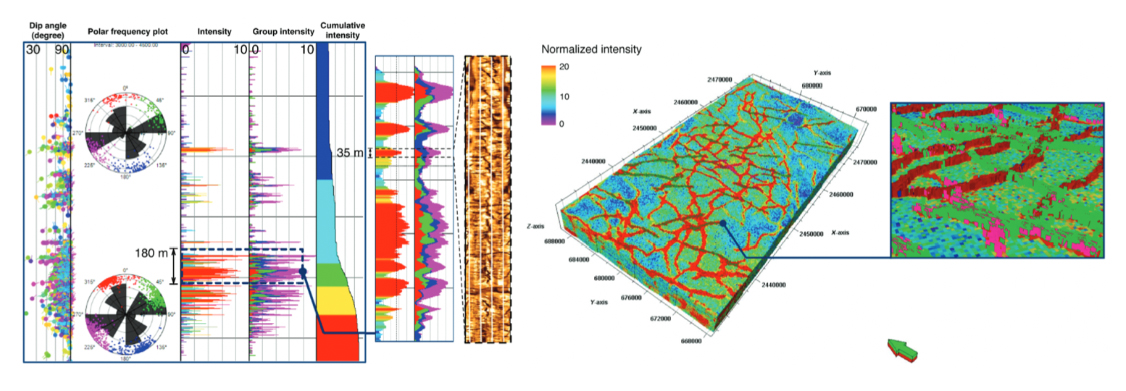
The prediction of natural fracture networks and their geomechanical properties remains a challenge for unconventional reservoir characterization. Because natural fractures are highly heterogeneous and of subseismic scale, integrating petrophysical data (i.e., cores and well logs) with seismic data is important for building a reliable natural fracture model. Therefore, our research group have developed an integrated and stochastic approach for discrete fracture network modeling with field data experimentation. In the method, we first perform a seismic attribute analysis to highlight the discontinuity in the seismic data. Then, extrapolate the well-log data that include localized but high-confidence information. By using the fracture intensity model including seismic and well logs, we can build the final natural fracture model that can be used as a background model for the subsequent geo-mechanical analysis such as simulation of hydraulic fractures propagation. As a result, our workflow combining multiscale data in a stochastic approach constructs a reliable natural fracture model.

We applied the generalized multiscale finite-element method (GMsFEM) to simulate seismic wave propagation in fractured media. Fractures are represented explicitly on a fine-scale tri-angular mesh, and they are incorporated using the linear-slip model. The motivation for applying GMsFEM is that it can re-duce computational costs by using basis functions computed from the fine-scale fracture model to simulate propagation on a coarse grid. First, we apply the method to a simple model that has a uniform distribution of parallel fractures. At low frequencies, the results could be predicted using a homogeneous, effective medium, but at higher frequencies, GMsFEM allows simulation of more complex, scattered wavefields generated by the fractures without assuming a specific form of anisotropy. A second, more complex model has two fracture corridors in addition to a few sparsely distributed fractures. Simulations compare scattered wavefields for different acquisition geometries. The third test case represents a vertical section of subsurface structures and is designed to test the influence of fractures on the surface seismic. We compared the fine-scale solution with multiscale solution to demonstrate the accuracy and efficiency of computations. Given the simulation results of three different test cases, GMsFEM allows a reduction of computation time of approximately 80% compared with a conventional finite-element result computed directly from the fine-scale grid, and it can predict seismic signal variations useful for the interpretation of fracture distributions.